Study Bay Coursework Assignment Writing Help

Summary:

This paper presents Novel VLSI (Very Giant Scale of Integration) structure for the QR decomposition (QRD) based mostly on the Modified Householder transformation (MHHT) algorithm. QRD of a matrix H is decomposition of matrixHright into a productof an orthogonal matrix Qand an higher triangularR. QRD is commonly used to resolve a number of engineering issues in lots of areas. Pre-processing modules based mostly on QRD makes the decoding in sign processing simpler and implementing knowledge detection with QRD helps to cut back the complexity of spatial multiplexing MIMO – OFDM detection. The strategies used for implementing QR decomposition are: Givens rotation, Modified GramSchmidt Orthogonalization (MGS), Householder Transformations (HHT), and certainly Modified Householder transformation (MHHT). The proposed MHHT algorithm reveals greatest trade-off between complexity and numerical precision, and likewise suites for VLSI architectures. The proposed MHHT algorithm reduces computation time and space of the QRD block in comparison with the prevailing Householder algorithm. Implementation of this algorithm is carried out in FPGA Virtex6 xc6vlx550tl-1Lff1759 system with the Helpance of Xilinx ISE 14.1.

Key phrases: MIMO methods,VLSI structure, QR Decomposition (QRD), Householder Transformation(HHT).

1. INTRODUCTION:

The QR decomposition (QRD) is a primary matrix factorization methodology from matrix-computation idea used to compute two output matrices Q and R from an enter matrix H, such that H = QR. QRD is commonly used to resolve many engineering areas like least-square issues, linear system equations and so on. For symbol-decoding options inside Spatial-Multiplexing A number of-Enter A number of-Output (SM-MIMO) methods, QRD principally consists in simplifying demodulation duties in suboptimal and near-optimal options by discovering an orthogonal matrix Q and an upper-triangular matrix R from an enter matrix H. A number of strategies in the direction of implementing the QRD are already reported in literature. As an example, and underneath the context of SM-MIMO methods, probably the most explored are the Modified Gram-Schmidt Orthogonalization (MGS, as a generalized enchancment of the Gram-Schmidt algorithm), Givens rotation, the Modified Householder Transformations (MHHT as an enhancement of the Householder Transformation algorithm). Because of its simplicity and numerical stability, the QR factorization algorithm using Householder transformations has been adopted. An outline of the principle steps of the Current Householder QR algorithm is offered. The aim of this work is to indicate that when modifying current Householder QR factorization to the matrix H, the computational complexity and space will get lowered. Because of its trade-off in complexity, numerical precision, and VLSI implementation suitability, the MHHT is most popular. The contribution of this paper is to current a versatile and scalable FPGA-based VLSI structure with aggressive capabilities towards different associated approaches, motivated on the context of SM-MIMO demodulation options.

The group of this paper is as follows:

Part II presents the QRD. In Part III, the exisiting HHT and MHHT algorithm is uncovered. Implementation outcomes are reported in Part IV, and conclusions are lined in Part V.

2. QR DECOMPOSITION

The QRD constitutes a related pre-processing operation in SM-MIMO demodulation duties [1-2]. The baseband equal mannequin might be described in

(1)

At every image time, a vector S with every image belonging to the Quadrature Amplitude Modulation (q-QAM) constellation passes via the channel response matrix H. The obtained vector y on the receiving antenna for every image time is a loud superimposition of the alerts contaminated by Additive White Gaussian Noise (AWGN) given by n.The utmost probability (ML) detector is the optimum detection algorithm for the MIMO system. It requires discovering the sign level from all transmit vector sign units that reduce the Euclidean distance with respect to the obtained sign vector. The transmitted image s might be estimated by fixing

(2)

This provides the optimum outcome. Nevertheless, fixing (2) with bigger constellations and a number of antennas will end in advanced calculations. As a substitute of fixing (2) as such, the image estimation might be simplified through the use of QR decomposition of.That’s the place resides the usefulness of decomposing matrix H in a QR type, yielding a back-recursive dependency on components in S with out incurring right into a BER (Bit Error Charge) loss [3-4]. With this follow, the computational complexity is lowered. The detected vector is computed based mostly on the ML algorithm with QR decomposition as given in (three)

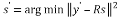(three)

the place

is in higher triangular type, approximation of is computationally easier with Helpance from (three). Notice that for MIMO-OFDM methods operated in stationary environments, the channel matrix stays virtually the identical. Thus, QR decomposition of the channel matrix might be finished solely as soon as to get matrix. Alternatively, the calculation of 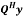should be up to date for each incoming sign.

2.1 QRD IMPLEMENTATION

The strategies used for QR decomposition are:

Gram–Schmidt algorithm obtains the orthogonal foundation spanning the column house of the matrix by the orthogonality precept. Utilizing a sequence of projection, subtraction, norm and division, the column vector of the unitary matrix containing the orthogonal foundation might be acquired one after the other and higher triangular matrix can also be obtained as a by-product. Householder Transformation (HHT) tries to zero out probably the most components of every column vector at a stroke by reflection operations. The higher triangular matrix is derived after every transformation matrix being utilized to each column vector sequentially. The unitary matrix includes the multiplications of those Householder transformation matrices and thus the complexity is way larger. Alternatively, Givens Rotation (GR) zeros one ingredient of the matrix at a time by two-dimensional rotation. If an identification matrix is fed as an enter, the unitary matrix might be calculated through the use of the identical rotation sequence when the higher triangular matrix is obtained (Malstev 2006; Hwang 2008 and Patel 2009).The Gram–Schmidt algorithm has the drawback that small imprecisions within the calculation of inside merchandise accumulate shortly and result in efficient lack of orthogonality.HHT methodology has larger numerical stabilitythan the Gram–Schmidt methodology. Givens methodology shops two numbers c and s, for every rotation and thus requires extra storage and work than Householder methodology .Givens rotation requires extra sophisticated implementation with the intention to overcome this disadvantages. Givens rotation might be useful for computing QR factorization solely when many entries of matrix are already zero, since nullifying sure matrix components might be skipped. In contrast to Givens Rework, Householder Rework can act on all columns of a matrix, and require much less computations for Tridiagonalization and QR decomposition, however can’t be deeply or effectively parallelized. Householder is used for dense matrices on sequential machines, whereas Givens is used for sparse matrices or/on parallel machines.

three. QRD utilizing Householder Transformation

On this part, the prevailing Householder Transformation algorithm is described, adopted by proposed HHT methodology structure is demonstrated intimately.

three.1 Householder Transformation

Householder QR algorithm progressively transforms H into an higher triangular type R by making use of a sequence of Householder matrices (multiplies H from the left with Q). Householder transformation is carried out by projecting a multi-dimensional enter vector onto a aircraft zeroes a number of components on the similar time. An n×n matrix H of the shape

, (four)

is known as a Householder matrix. The vector 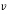is known as a Householder vector. Pre-multiplication of the coefficient matrix 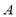with 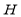is used to zero out applicable components of. It’s simple to confirm that Householder matrices are symmetric and orthogonal.

The Householder matrix block includes the computation of an outer product which requires complexity operation. Nevertheless, the sensible time requirement of utilizing 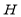to zero out components in 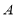is decrease than that of computing a full outer product. That is due to the tedious computation of the total matrix 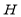which isn’t crucial in follow.

Householder reflections work nicely for introducing giant variety of zeros utilizing only one matrix multiplication (computing). Usually, all the weather under the diagonal of a whole column of the matrix 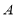are eradicated by one Householder reflection. Nevertheless, this results in a problem when Householder transforms are carried out on parallelly. One reflection impacts a number of rows, and due to this fact, it’s tough to attain fine-grained parallelism within the operation.

The algorithm for Householder remodel is given in Desk 1. and its block diagram is given in Determine 2.

Fig. 2 Block diagram of HHT

Desk 1 HHT algorithm

Householder vector block:

The standard methodology of Householder algorithm for decomposing channel matrix is given in Desk 1. Initially, the channel matrix 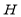is assigned to matrix. It may be periodically up to date by following steps to acquire higher triangular matrix. The primary column of 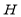is assigned to ‘a’ vector. After that the norm worth of ‘a’ is calculated and assigned it to ‘g’. The Householder vector ‘v’ is the division ‘u’ and‘t’ which is the norm operation of vector choice .

Householder matrix block:

The output of Householder vector is given as enter to Householder matrix block. Lastly, H is computed by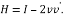

The above operation might be up to date upto n occasions to acquire the higher triangular matrix and unitary matrix. It’s given under,

(5)

Q = (H_nH_n-1…H₁) ^T (6)

Right here the matrix is given to the enter of channel matrix to replace its vector worth. The orthogonal matrix is computed by the multiplication of ‘n’ Householder matrix. Therefore its complexity will increase and likewise it occupy extra space. If the matrix measurement will increase, the space additionally will increase tremendously. So there’s want to cut back the complexity of this block.

three.2 Proposed HHT methodology

The prevailing methodology of Householder reflection requires giant space and computation time. Householder transformations additionally present the potential of nullifying a number of components concurrently by reflecting a multi-dimensional enter vector onto a aircraft. Nevertheless, VLSI implementation of the Householder algorithm wants square-root, multiplication and division operations, which require excessive complexity. To resolve this concern, a novel Householder algorithm is offered that use sequence of easy Householder projections, which might be simply carried out utilizing easy arithmetic operations.

The proposed algorithm as given in table2 has lesser variety of computations in comparison with the prevailing algorithm. In Determine three, the block diagram of modified methodology is given. It reveals two main sub blocks (i.e.) householder vector block and householder matrix block. Householder vector block is similar to the earlier methodology of computing ‘v’ with further weight vector computation. Right here modification taken within the Householder matrix block to remove matrix multiplication. The vector ‘v’ subtracted from ‘f’ and column vector of channel matrix to offer ‘H’ worth.

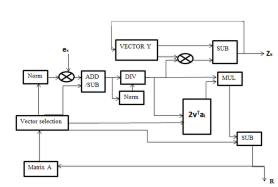
Fig. three Block diagram of MHHT.

In step one, matrix H is lowered to with all zeros under the diagonal ingredient within the first column by computing the signal of the pivot ingredient d and weight worth w. In comparison with the earlier algorithm, variety of steps required to acquire the primary matrix might be lowered. For instance, if the preliminary channel matrix of four×four undergone to Householder reflection, then it reduces the matrix with all zeros under the primary ingredient. The computation of Householder vector 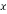within the current algorithm requires giant reminiscence and space. As a result of 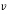is a four×four matrix, multiplication of turn into advanced course of. To keep away from such a process, column vector of matrix has been taken one after the other and course of it iteratively to acquire the higher triangular matrix. After computation of step one the matrix measurement lowered to. After that, the sub matrix of measurement three×three is taken and the steps might be utilized repeatedly.

The algorithm to compute Householder Vector block is given under.

Desk 2 HHT algorithm

Householder vector block:

On this Householder reflection algorithm, it transforms the column

(7)

into the vector of the shape

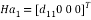(eight)

the place the diagonal ingredient

(9)

The Householder vector might be computed by,

(10)

the place

and

This block computation is similar as that of earlier Householder vector block with a bit of modification within the weight worth.

Householder matrix block:

After acquiring the Householder vector, the output vector is given to the enter of Householder matrix block. The computation of this block may be very easy in comparison with earlier methodology of Householder matrix block computing. The Householder matrix ingredient algorithm is given under,

(11)

the place

It reduces the channel matrix to its higher triangular type in steps. To cut back the complexity of computing Q, right here the output vector y’ has been taken straight and its algorithm is given under,

(12)

So the execution time for computing the higher triangular matrix and output vector may be very much less when in comparison with typical Householder reflection algorithm. This reduces the space for the Householder matrix block. The QR decomposition utilizing modified Householder transformation algorithm is simulated by taking ‘a’ as enter channel matrix, ‘zb’ as output vector and ‘higher’ as higher triangular matrix. The unitary or orthogonal matrix ‘Q’ want to not be calculated. The output vector 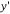in (three) might be computed from the up to date Householder vector ‘v’. Additionally the additional time wanted to calculate ‘Q’ might be lowered. So the pace of decomposing the channel matrix might be elevated tremendously.

four. Outcomes and Dialogue

QR decomposition algorithm is required as a pre-processing unit for many MIMO detectors. The accuracy of the channel matrix QR decomposition doesn’t have an effect on the MIMO detection course of and at last receiver’s bit-error-rate (BER) efficiency. The prevailing and proposed Householder algorithms are downloaded on to Xilinx system xc6vlx550tl-1Lff1759. The synthesis outcomes are in comparison with present the world effectivity of the proposed one.

The channel matrix H components are represented in floating level illustration of 16 bits comprising 1 for signal bit,three bits for decimal half and 12 bits for fractional half. The 16 bit illustration reveals an numerical precision oscillates across the interval[10^-6,10^-5] for each current and modified algorithms .

The computation of column vectors of the R matrix might be parallelised in modified algorithm and thus enchancment is obtained in computational time of 49.7% discount.The computational time for proposed algorithm is about 194.84ns,whereas exisiting algorithm is about 394.56ns.

Modified algorithm reduces the matrix computation into vector multilications for some extent and thus reduces the space as obtained from the synthesis report.

Desk three Synthesis report for Standard Householder algorithm

Desk four Synthesis report for Proposed Householder algorithm

Desk 5 Comparability outcome

5. Conclusion

To cut back the computational and complexity, Householder transformation algorithm for QRD has been modified. The computation of Q is the tedious course of within the current algorithm. On this work, it may be overcome by straight computing output vector. It reduces the computation time by 52.38% and likewise cut back in space in comparison with earlier HHT algorithm (Slices – 31%, LUTs – 49.eight%) offered within the QRD. Thus it’s evident from the comparability outcome that the variety of slices and four enter LUTs required in FPGA implementation of QR Decomposition is lowered thereby making the low advanced design which may meet the specs of most OFDM communication methods, together with VDSL, 802.16, DAB and DVB. In future, this work might be prolonged to implement Ok-best LSD and Turbo decoding of LTE receiver.

References

1. Lee, Ok.F. and Williams, D.B.: An area-frequency transmitter variety approach for OFDM methods. In Proc. World Telecommunications Conf., San Francisco, CA, pp. 1473-1477. (Nov. 2000)
2. H. Kim, J. Kim, S. Yang, M. Hong, and Y. Shin, “An efficient MIMO–OFDM system for IEEE 802.22 WRAN channels,” IEEE Trans. Circuits Syst. II, Exp. Briefs, vol. 55, no. eight, pp. 821–825, Aug. 2008.
3. H.-L. Lin, R. C. Chang, and H.-L. Chen, “A excessive pace SDM-MIMO decoder utilizing environment friendly candidate looking out for wi-fi communication,” IEEE Trans. Circuits Syst. II, Exp. Briefs, vol. 55, no. three, pp. 289–293, Mar. 2008.
4. L. Boher, R. Rabineau, and M. Helard, “FPGA implementation of an iterative receiver for MIMO–OFDM methods,” IEEE J. Sel. Areas Commun., vol. 26, no. 6, pp. 857–866, Aug. 2008.
5. M.-S. Baek, Y.-H. You, and H.-Ok. Track, “Mixed QRD-M and DFE detection approach for easy and environment friendly sign detection in MIMO–OFDM methods,” IEEE Trans. Wi-fi Commun., vol.
6. eight, no. four, pp. 1632–1638, Apr. 2009.
7. C. F. T. Tang, Ok. J. R. Liu, and S. A. Tretter, “On systolic arrays for recursive advanced Householder transformations with functions to array processing,” in Proc. Int. Conf. Acoustics, Speech, and Sign Course of., 1991, pp. 1033–1036.
8. Ok.-L. Chung and W.-M. Yan, “The advanced Householder remodel,” IEEE Trans. Sign Course of., vol. 45, no. 9, pp. 2374–2376, Sep. 1997.
9. S. Y. Kung, VLSI Array Processors. Higher Saddle River, NJ, USA: Prentice-Corridor, 1987.